Resumen
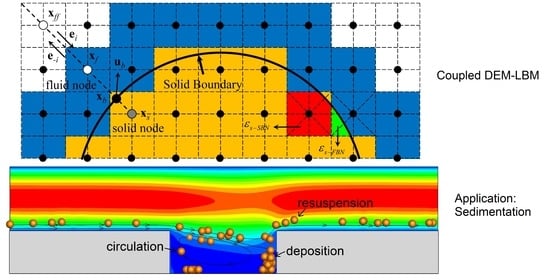
Particle?fluid flows are ubiquitous in nature and industry. Understanding the dynamic behaviour of these complex flows becomes a rapidly developing interdisciplinary research focus. In this work, a numerical modelling approach for complex particle?fluid flows using the discrete element method coupled with the lattice Boltzmann method (DEM-LBM) is presented. The discrete element method and the lattice Boltzmann method, as well as the coupling techniques, are discussed in detail. The DEM-LBM is thoroughly validated for typical benchmark cases: the single-phase Poiseuille flow, the gravitational settling and the drag force on a fixed particle. In order to demonstrate the potential and applicability of DEM-LBM, three case studies are performed, which include the inertial migration of dense particle suspensions, the agglomeration of adhesive particle flows in channel flow and the sedimentation of particles in cavity flow. It is shown that DEM-LBM is a robust numerical approach for analysing complex particle?fluid flows.